デジタル計測の基礎
前回はパワー半導体について紹介し、性能が向上してきたことを紹介しました。そして性能の向上には幾つかの観点での数値測定が必要で、そのためにテスト機器も性能を向上させなければならないということも紹介しました。実は、パワー半導体の計測だけではなく、数値測定の技術自体がこの数年、一気に注目されてきています。そのキーワードは「IoT(Internet of Things)」です。
計測を行う機器の大きな変化としては、1950年代から進んできたアナログ計測器からデジタル計測器への変化があります。電流計や電圧計を思い出してもらえば良いのですが、中学校や高校で理科の実験の際に使ったものは針が振れるタイプのアナログ式だったと思います。しかし、アナログ式では最も細かい目盛の10分の1までを読み取ることが求められますが、それ以上に細かい数値を読む事はできません。理科の実験程度であればそれでも十分だったのかも知れませんが、半導体の設計とその性能評価においては、不十分なのです。
そのため現場ではデジタル式の計測器が主流となり、表示だけではなく計測部分もデジタル化が進んでいます。
基本的にはセンサで得られた情報をA/D変換を行うことでデジタル化します。その計測できる対象は多岐にわたっていて、現在では電流、電圧、抵抗値、周波数、温度、湿度、照度(光)、pH、圧力、音、距離、地磁気、加速度、ジャイロなどの値をデジタルで取得することができます。
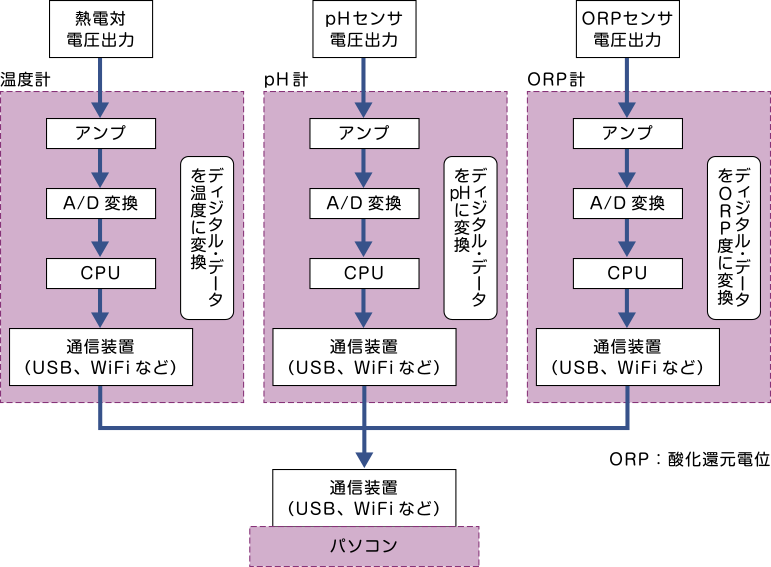
このように、各センサで取得されたアナログ値は電圧として出力されます。その後、アンプでの増幅やA/D変換を経てパソコンなどに取り込まれます。上の図では電圧として出力されるセンサの例を挙げましたが、シーケンサやデジカメなどで使われるイメージセンサなどは、(積算)電流値を入力値としてA/D変換しています。
近年ではセンサとパソコン(場合によってはタブレットやスマートフォン)の間の通信は、USBや無線で行われる事が多くなっています。特に屋外設置型のセンサの場合(デジタル百葉箱など)で、通信用のケーブル敷設が難しい場合は、無線によるデータのアップロードが中心になっています。また、直接インターネット上に設置されたサーバーにデータがアップロードされるケースもあります。
こういうことができるようになった背景には、以前と比較すると同じ処理をするのに必要なコンピュータのサイズが小さくなってきたことがあります。SoC(System on Chip)技術の進歩は早く、一昔前のPCが1㎝角のチップの中に納まるようになっているのです。これにより太陽電池や乾電池でも十分に動作するほど省電力になり、無線が使えるチップであっても千円も出せば買えるようになっています。つまり、使い捨てても大丈夫なくらい、センサと処理するコンピュータのセットが安くなっているのです。
同様に無線通信の方も、3Gや4Gの携帯電話回線基地局が整備されているため、無線LANではなく、携帯電話回線を利用したデータ通信が主流となってきています。非常に省電力で通信ができるSIGFOXやLoRa、NB-IoTなどのLPWA(Low Power Wide Area)規格の策定も行われ、何百地点もの温度や湿度などをA/D変換でデジタルデータにできさえすれば、直接携帯電話回線を通してインターネット上のサーバーに送り、このデータを集約処理することが容易な時代になっています。
集めたデータはビッグデータとして分野に応じた情報処理が行われ、社会インフラ監視、災害予防や農業の省力化など、様々に応用されています。IoTは、こういったデータの活用が進んできたことで、近年注目されるようになってきました。
では、このようなセンサからPCにデータが渡されるまでの、データ数値の変化を見てみましょう。ここではpHセンサを例にします。
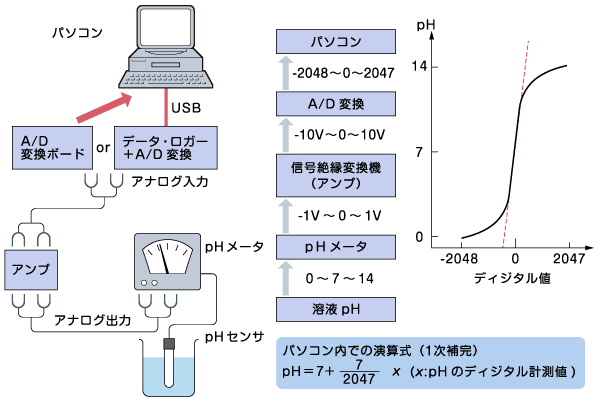
このようにpHセンサで計測された値は、pHメータに渡される際に0~14の間の数値になります。この際の値はアナログ形式です。
そこで一旦-1V~1Vの範囲の電圧に変換され、信号絶縁変換器(アンプ)に送られます。アンプ内ではそれを-10V~10Vに増幅されます。ここまでがアナログデータです。
ここでA/D変換が行われます。その結果、-10V~10Vだったアナログ値は、-2048~2047(2の乗数であればもっと大きくても構いません)のデジタル値に変換された後、パソコンなどに送られます。もちろんパソコンに送る前段階で、もう一度0~14のデジタル値に変換し直しても構いません。いずれにせよ、アナログ値は一旦電圧に変換された後、デジタル値へと変わるのです。
もし入力が電流であった場合、例えばシーケンサでは直流の0~20mAを入力値として、これをA/D変換して利用することが多いようです。
計測の細かさ(分解能)
さて、アナログ値をデジタル値へと変換する流れはわかっていただけたと思います。しかし、これらを計測するにあたっては、その細かさが大変重要になります。先ほど-2048~2047に変換すると書きましたが、2の乗数であればもっと大きな数字でも構いません。何故2の乗数かというと、コンピュータでは「0か1」という情報の単位である1bit(ビット)を基本的な情報の単位として扱っているためで、先ほどの2048という数字は211ということになり、これを「11bit」と呼びます。さらに先頭にプラスかマイナスかを判別するビット(0だと正数、1だと負数)を1つ追加で入れて12bitにすることにより、「111111111111」ならば「-2048」、「011111111111」ならば「2047」として書くことができます。
| bit | 10進数表記での範囲 | |||||
|---|---|---|---|---|---|---|
| 符号あり | 符号なし | 分解能 | 段階当たりの電圧値 (10VFSの場合) |
%FS | dBFS | |
| 2 | -2~1 | 0~3 | 4 | 2.5V | 25 | -12 |
| 3 | -4~3 | 0~7 | 8 | 1.25V | 12.5 | -18 |
| 4 | -8~7 | 0~15 | 16 | 0.625V(625mV) | 6.25 | -24 |
| 5 | -16~15 | 0~31 | 32 | 0.313V(625mV) | 3.12 | -30 |
| 6 | -32~31 | 0~63 | 64 | 0.156V(156mV) | 1.56 | -36 |
| 7 | -64~63 | 0~127 | 128 | 0.0781V(78.1mV) | 0.78 | -42 |
| 8 | -128~127 | 0~255 | 256 | 0.0391V(39.1mV) | 0.39 | -48 |
| 9 | -256~255 | 0~511 | 512 | 0.020V(20mV) | 0.2 | -54 |
| 10 | -512~511 | 0~1023 | 1024 | 0.00977V(9.77mV) | 0.098 | -60 |
| 11 | -1024~1023 | 0~2047 | 2048 | 0.00488V(4.88mv) | 0.049 | -66 |
| 12 | -2048~2047 | 0~4095 | 4096 | 0.00244V(2.44mV) | 0.024 | -72 |
| 13 | -4096~4095 | 0~8191 | 8192 | 0.00122V(1.22mV) | 0.012 | -78 |
| 14 | -8192~8191 | 0~16383 | 16384 | 0.000610V(610μV) | 0.0061 | -84 |
| 15 | -16384~16383 | 0~32767 | 32768 | 0.000305V(305μV) | 0.003 | -90 |
| 16 | -32768~32767 | 0~65535 | 65536 | 0.000153V(153μV) | 0.0015 | -96 |
| 17 | -65536~65535 | 0~131072 | 131071 | 0.000076V(76μV) | 0.0008 | -102 |
| 18 | -131072~131071 | 0~262143 | 262144 | 0.000038V(38μV) | 0.0004 | -108 |
| 19 | -262144~262143 | 0~524287 | 524288 | 0.000019V(19μV) | 0.0002 | -114 |
| 20 | -524288~524287 | 0~1048575 | 1048576 | 0.00000954V(9.54μV) | 0.0001 | -120 |
| 21 | -1048576~1048575 | 0~2097151 | 2097152 | 0.00000476V(4.76μV) | 0.000048 | -126 |
| 22 | -2097152~2097151 | 0~4194303 | 4194304 | 0.00000238V(2.38μV) | 0.000024 | -132 |
| 23 | -4194304~4194303 | 0~8388607 | 8388608 | 0.00000119V(1.19μV) | 0.000012 | -138 |
| 24 | -8388608~8388607 | 0~16777215 | 16777216 | 0.000000596V(596nV) | 0.000006 | -144 |
| 25 | -16777216~16777215 | 0~33554431 | 33554432 | 0.000000298V(298nV) | 0.000003 | -151 |
| 26 | -33554432~33554431 | 0~67108863 | 67108864 | 0.000000149V(149nV) | 0.000002 | -157 |
| 27 | -67108864~67108863 | 0~134217727 | 134217728 | 0.0000000745V(74.5nV) | 0.0000007 | -163 |
| 28 | -134217728~134217727 | 0~268435455 | 268435456 | 0.0000000373V(37.3nV) | 0.0000004 | -169 |
| 29 | -268435456~268435455 | 0~536870911 | 536870912 | 0.0000000186V(18.6nV) | 0.00000002 | -175 |
| 30 | -536870912~536870911 | 0~1073741823 | 1073741824 | 0.0000000093V(9.3nV) | 0.000000009 | -181 |
| 31 | -1073741824~1073741823 | 0~2147483647 | 2147483648 | 0.0000000047V(4.7nV) | 0.000000004 | -187 |
| 32 | -2147483648~2147483647 | 0~4294967295 | 4294967296 | 0.0000000023V(2.3nV) | 0.000000002 | -193 |
この数字が大きくなるということは、それだけ-10V~10Vの値を細かく分解できるということを意味しているからです。この細かさを「分解能」と言います。
近年の計測機器では、より高い精度の計測値や誤差を求められることが増えて来ました。そのため分解能は高い方がより細かい計測ができるため、制作にあたってはどれくらいの分解能を目標とするのかが重要な開発要件となります。またテストを行う側も、必要な分解能をしっかりと設定しなければ、正しい計測機材を選定できないため、分解能の設定は大変重要です。
下の図は分解能が低い場合と高い場合の比較です。
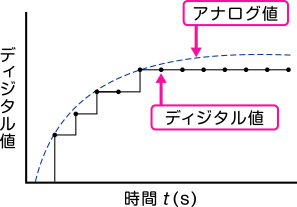
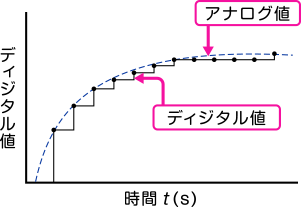
これはアナログ値の時間変化をグラフにしたものです。見てわかるとおり、一番左のアナログ値の変動をデジタル値へと変換した場合、真ん中のグラフ(低分解能)よりも右端のグラフ(高分解能)の方が、よりアナログ値に近い値を出していることがわかります。従って、分解能は高い方がより正確になります。
また、横軸の時間に対しても同様の事が言えます。できる限り短い時間でデータを出力すれば、変化を細かく計測することができます。この場合、コンピュータやA/D変換ボードの処理速度が向上しましたので、10年前や20年前と比較すると、格段に短い時間で計測することが可能になっています。
ただし単純に短くすれば良いというわけではありません。計測する元の入力が少ない場合、短い時間だと計測値のブレや誤差が大きくなります。例えば、暗い所で写真を撮ることを考えれば良いでしょう。暗い場所ではセンサに入ってくる光の量が少なくなるため、短い時間で写真を撮ると全体的に荒れた写真になってしまいます。つまり、計測する対象物の量がそもそも少ない場合、一定時間に平均して10だけしか入力がない場合、たまたま11の入力があると、値が1.1倍になってしまいます。入力が10000ある場合ですと、10001になってもほとんど気にしなくて良いレベルだという事が分かります。
従って、計測タイミングや、計測に用いる積分(積算)時間などは、慎重に考える必要があります。電圧値や電流値の計測、スイッチングタイミングの計測、抵抗値の計測、動作環境温度の計測などを行う場合に、どの様な設計が必要なのか、どの様な計測のパターンがあり得るのかを考えることが大切なのです。
参考文献
- トランジスタ技術SPECIAL No.53 Winter
- 計測と制御 第41巻第1号 2002年1月号「歴史が選んだ計測器」
https://www.jstage.jst.go.jp/article/sicejl1962/41/1/41_1_53/_pdf - 東北大学大学院情報科学研究科 鏡慎吾 「イメージセンサの基礎」
http://www.ic.is.tohoku.ac.jp/~swk/lecture/ic2005/kagami_ic20050419.pdf - シーケンス制御講座「アナログ変換」
https://news.aperza.jp/シーケンス制御講座「アナログ変換」/




 0120-747-636
0120-747-636